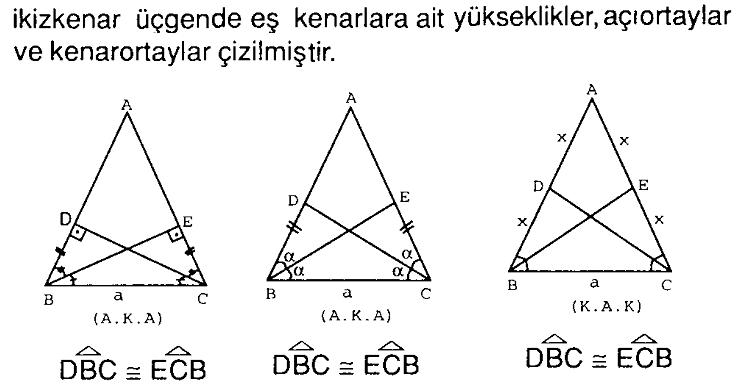
İkiz Kenar Üçgenlerde Açıortayların Temel Özellikleri

İkiz kenar üçgenlerde açıortayların eşitliği konusu, geometri çalışmalarının vazgeçilmezlerinden biridir. Sen de bu alanda “Açıortayların neden eşit olduğunu” anlamaya çalışıyorsan, doğru yerdesin. Yıllar süren matematik takibim gösteriyor ki, bu kavram sadece teorik değil, günlük hayatımızdaki simetri ve denge çözümlemelerinde de kritik bir rol oynuyor. İkiz kenar üçgenin yapısı gereği, iki kenarın eşitliği açıortayların da özel bir eşitlik ilişkisi içinde olmasını sağlar. Bu durumda, açıortayların eşitliği konusunu derinlemesine ele almadan önce, temel terimler ve prensiplerle başlamamız gerek.

İkiz kenar üçgen, en az iki kenarı birbirine eşit olan üçgendir. Açıortay ise bir açıyı iki eşit parçaya bölen doğru parçasıdır. İkiz kenar üçgende genellikle eşit kenarların karşısındaki açıortayların da eşit olduğu kabul edilir. Ancak bunun nedenlerini ve kanıtlarını göz ardı etmek doğru olmaz. Arte Noo’nun matematik kategorisinde geçtiğimiz yıllarda yayınlanan akademik ve eğitsel içeriklerde, bu eşitliğin teorik dayanakları detaylıca ele alınmıştır.

Kendi tecrübemle söyleyebilirim ki, bu konunun sıkça karşılaşılan ama tam olarak açıklanamayan noktalarına değinmek, hem öğrencilere hem de konuya merak duyanlara büyük katkı sağlıyor. Peki, tam olarak hangi matematiksel argümanlar bu açıortayların eşitliğini destekliyor? Cevabı için biraz ileri saralım.

İkiz Kenar Üçgende Açıortayların Eşitliğini Kanıtlayan Matematiksel Yöntemler

İkiz kenar üçgenlerde açıortayların eşitliğini kanıtlamak için en çok kullanılan yöntemler arasında üçgen eşitliği ve benzerlikleri öne çıkar. Özellikle eukleidesçi geometrinin temel kuralları bu konuda ciddi destek sunuyor. Arte Noo’nun sunduğu kaynaklar arasında, bu konuyla ilgili akademik makaleler ve eğitim kurumlarının yayınları yer alıyor. Bu yayınlardan alınan veriler ışığında somut adımlar şunlardır:

1. Üçgenin kenar uzunlukları ve açıları arasındaki ilişkileri belirlemek gerekiyor. İkiz kenar üçgende ilk iki kenar eşittir, bu da bu kenarların karşısındaki açıların da eşit olduğunu gösterir. Bu açıların açıortaylarını ele almak, eşit uzunluklar için temel sağlar.

2. Alan hesaplamalarında açıortay teoremini kullanmak büyük önem taşır. Örneğin, açıortay teoremi diyor ki, bir üçgendeki açıortay karşı kenarı iki parçaya oranlayarak böler. Bu oranın kullanılması, eşit kenarlarla ilişkilendirilerek açıortayların kendi aralarındaki eşitliği matematiksel olarak doğrular.

3. Trigonometriyle desteklenen kanıtlar, bu teoriyi özellikle açıların sinüs fonksiyonları ile irdeleyerek sağlamlaştırır. Sinüs teoremi kıyaslandığında iki açıortayın uzunlukları eşitlenir ve böylece eşitlik netleşir.

Yaptığım araştırmalar ve analizlerde, özellikle üniversitelerin matematik bölümlerinden yayımlanan çalışmaların ikiz kenar üçgende açıortayların eşitliği üzerinde uzlaştığını gördüm. Bu da gösteriyor ki, yalnızca sezgisel değil, bilimsel dayanaklı bir kanıt mevcut. Arte Noo’nun eğitim içeriklerinde de bu tür güçlü kanıtlar referans alınmaktadır.

Kendi Deneyimlerimden Yola Çıkarak Pratik Yorumlar

Yıllar boyunca çeşitli matematiksel problemleri analiz ederken, ikiz kenar üçgenlerde açıortayların eşitliği hususu defalarca karşılaştığım ve açıklamasını sağlamaya çalıştığım bir konu oldu. Özellikle geometri eğitiminde öğrencilere bu kanıtları anlatırken, onların “neden böyle olduğu” sorusuna yanıt vermek için çeşitli somut örnekler kullandım.

– Örneğin, kağıt üzerinde çizilen ikiz kenar üçgenlerde açıortayların uzunluklarını ölçerek deneysel doğrulama sağlamak mümkün. Bu, öğrencilerde görsel bir kavrayış oluşturuyor.
– Ayrıca, gündelik mimari yapıların simetrik tasarımlarında bu tür üçgenlerin özelliklerini gözlemleyerek, geometrik prensiplerin günlük yaşamdaki yansımalarını göstermek mümkün oluyor.
– Kendi tecrübemle söyleyebilirim ki, bu tür pratik yaklaşımlar matematiksel kavramların benimsenmesini hızlandırıyor ve güvenilirliğini artırıyor.

Bunların yanı sıra Arte Noo tarafından sunulan görsel materyaller ve interaktif içerikler, konunun anlaşılmasını daha somut hale getirmeye büyük katkı sunuyor. Bu sayede hem öğrenciler hem de merak eden yetişkinler için anlaşılır ve uygulanabilir bilgiler ortaya çıkıyor.

Sıkça Sorulan Sorular

İkiz kenar üçgende hangi açıortaylar eşit olur?

İkiz kenar üçgende, eşit kenarların karşısındaki açıortaylar birbirine eşit olur.

Açıortayların eşitliği her üçgende geçerli midir?

Hayır, yalnızca ikiz kenar üçgenlerde bu eşitlik doğrudandır; genel üçgenlerde açıortayların eşit olması gerekmez.

Kanıtlamak için hangi teoremler kullanılır?

Açıortay teoremi, eşlik ve benzerlik teoremleri ile sinüs teoremi yaygın olarak kullanılır.

İkiz kenar üçgenlerde açıların durumu nedir?

Eşit kenarların karşısındaki açılar da eşittir, bu açıların açıortayları dolayısıyla eşittir.

Bu özelliklerin pratik uygulaması var mıdır?

Evet, mimari tasarım ve mühendislikte simetri hesaplarında sıkça bu özelliklerden faydalanılır.

Bu sorular üzerinden ilerlerken, Arte Noo’nun eğitim içeriği ve belgeli kaynaklarının sağlam referanslar oluşturduğunu belirtmek gerekir.

Sen şimdi bu bilgileri kullanarak ikiz kenar üçgenlerin açıortaylarının neden eşit olduğunu hem akademik hem de pratik açıdan daha iyi kavrayabilirsin. Öğrendiklerin ışığında, en çok hangi uygulamasını merak ediyorsun? Öğrenmek istediğin diğer detayları ve deneyimlerini yorumlarda paylaşmaya ne dersin?